Introduction to Artificial Neural Networks
Artificial Neural Networks (ANNs) are computational models inspired by the human brain, designed to recognize patterns and solve complex problems in machine learning. These networks consist of interconnected nodes, or neurons, that work in unison to process information, much like the synapses and neurons in biological systems. The fundamental purpose of ANNs is to learn from data, enabling them to make predictions or decisions without explicit programming for every task.
The structure of an ANN typically includes an input layer, one or more hidden layers, and an output layer. Each layer consists of multiple nodes that perform calculations on input data, passing outputs to subsequent layers. The connections between these nodes have associated weights, which are adjusted during training to minimize errors in predictions. This weight adjustment process is commonly implemented through backpropagation and optimization techniques such as gradient descent.
Artificial Neural Networks are essential in various applications, from image and speech recognition to natural language processing and autonomous systems. Their ability to analyze vast amounts of data and learn intricate patterns allows them to perform tasks that traditional algorithms may struggle with. As technology advances, the importance of ANNs continues to grow, enabling breakthroughs in numerous fields such as healthcare, finance, and robotics.
The biological inspiration behind ANNs is a key asset to their functionality, as it allows them to mimic the learning processes of the human brain. By understanding the principles of perception, abstraction, and decision-making inherent to neural systems, researchers can enhance the design and effectiveness of artificial networks. This synthesis of biological research and computational theory is pivotal in advancing the capabilities of machine learning, showcasing the potential of artificial neural networks in transforming the way we interact with technology.
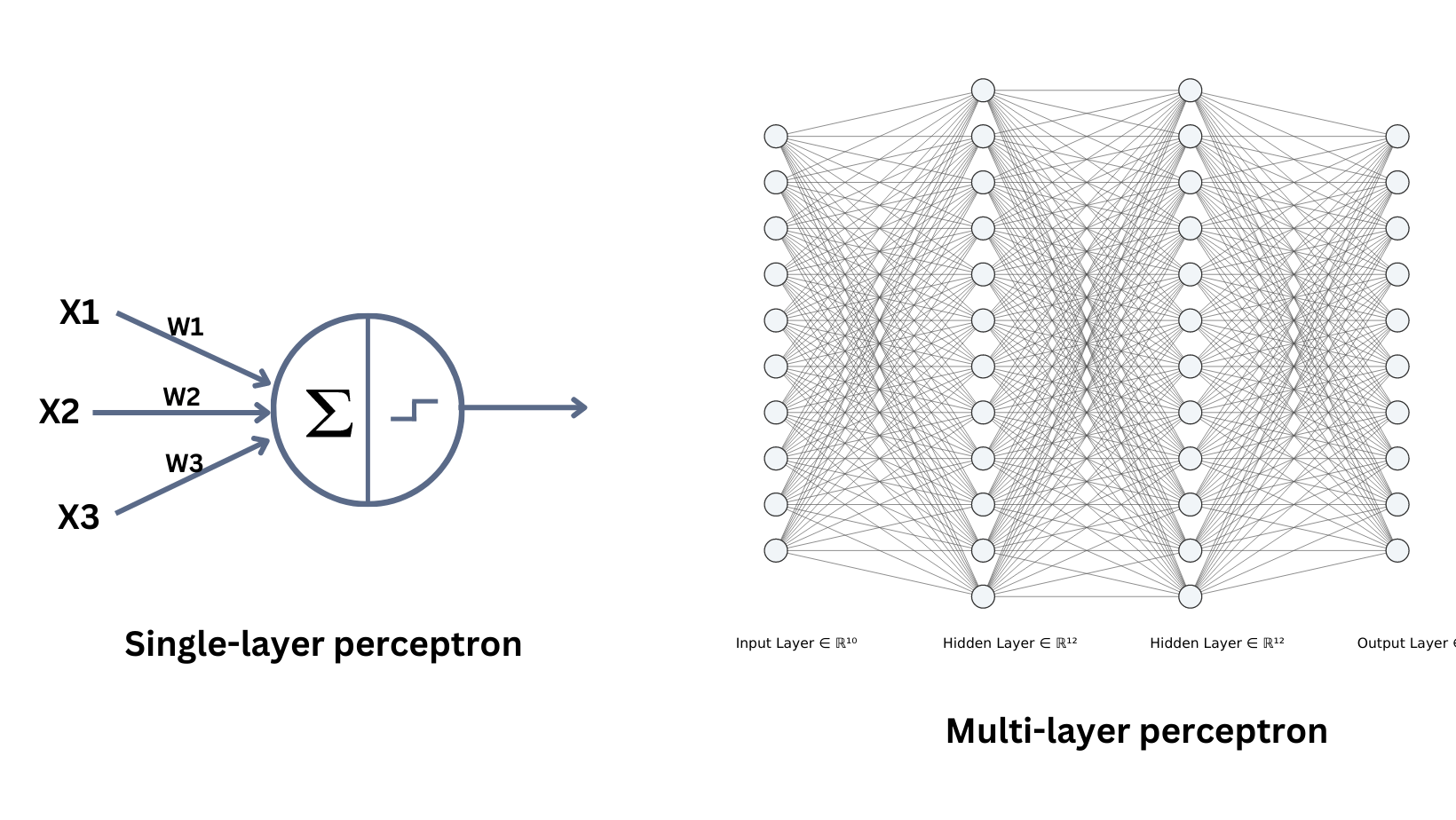
The Basic Building Block: The Perceptron
The perceptron stands as the foundational element of artificial neural networks, embodying the simplest form of a neural computation model. Developed by Frank Rosenblatt in the late 1950s, the perceptron is intended to simulate the functionality of a single neuron within the human brain. Like biological neurons, the perceptron receives inputs, applies weights, and produces an output based on a specific activation function.
At its core, the perceptron consists of several key components: inputs, weights, a bias, and an output function. Inputs represent the features or attributes of the data that the model processes. Each input is assigned a weight, which indicates its relative importance in the decision-making process. Adjusting these weights allows the perceptron to learn from the data by enhancing or reducing the influence of certain inputs based on feedback from the output.
The bias serves as an additional parameter that allows the model to shift the activation function’s threshold, offering further control over the output even when all input values are zero. This aspect is crucial as it provides the perceptron with flexibility, making it capable of modeling more complex relationships in the data. The output function, typically a step function or a sigmoid function, determines the final output based on the weighted sum of inputs combined with the bias. This center point of calculation is essential for classification tasks, where the perceptron can decide between two categories.
In essence, the perceptron forms the nucleus of artificial neural networks, serving as an ideal building block for more complex models. It encapsulates the fundamental principles of neural function through its architecture, thereby paving the way for advancements in deep learning and broader implementations across diverse applications.
Mathematical Foundations of the Perceptron
At the core of perceptron functionality lies its mathematical framework, which facilitates various operations essential for data classification. The perceptron, being a type of artificial neural network, utilizes linear combinations of inputs to produce outputs. The fundamental equation governing this operation can be expressed as:
y = f(w x + b)
In this formulation, w represents the weight vector associated with each input feature, x corresponds to the input vector, b signifies the bias, and f denotes an activation function. The linear combination, w x + b, computes a weighted sum of inputs, which is then processed by the activation function to yield the perceptron’s output.
The activation function plays a critical role in determining the output based on the input value. Commonly employed functions include the step function and sigmoid function. The step function outputs binary results, essential for binary classification tasks, while the sigmoid function allows for smoother transitions and can be used for probabilistic interpretations.
Understanding the concept of linear separability is crucial in perceptron operation. A dataset is deemed linearly separable if a hyperplane can be formed that distinctly separates two classes in the feature space. However, perceptrons are limited to datasets that meet this criterion. In situations where data is not linearly separable, perceptrons struggle to classify effectively, highlighting the necessity for more advanced architectures, such as multi-layer neural networks.
Thus, the mathematical foundations of perceptrons, characterized by linear combinations and specific activation functions, establish the groundwork for their classification capabilities. Despite their simplicity, these components render perceptrons invaluable for understanding more sophisticated structures within artificial intelligence frameworks.
The Geometry of Perceptrons
The perceptron, as a fundamental building block of artificial neural networks, inherently relies on geometric principles to achieve its classification tasks. At its core, the perceptron operates within a multi-dimensional space, where each feature of input data represents a unique dimension. The classification decisions made by a perceptron can be understood through the lens of hyperplanes, which act as boundaries separating different classes.
A hyperplane in an n-dimensional space can be described mathematically as the set of points that satisfy a linear equation, essentially defining the demarcation between distinct categories of data. For a perceptron, its decision-making process hinges on the ability to find an optimal hyperplane that divides the dataset into separate regions corresponding to the different classes. Thus, the learning process involves adjusting the weights attributed to each input feature to refine the orientation and position of the hyperplane.
The implications of this geometric approach are significant, particularly as the dimensionality of the data increases. In higher-dimensional spaces, the potential for complex relationships between features grows, complicating the linear separability of classes. Consequently, when input data is not linearly separable, a single layer perceptron becomes ineffective. This limitation led to the development of multi-layer perceptrons and advanced structures that leverage geometric properties to classify non-linear datasets effectively.
Understanding the geometry of perceptrons not only illuminates the mechanics behind their functionality but also emphasizes the importance of feature selection and transformation in machine learning applications. By visualizing data in a geometric context, practitioners can better appreciate how perceptrons relate to the concepts of classification boundaries and decision-making processes in artificial intelligence.
Learning Mechanism: Gradient Descent and Backpropagation
The learning mechanism employed by perceptrons is fundamentally rooted in two key processes: gradient descent and backpropagation. Understanding these mechanisms is crucial for comprehending how perceptrons adjust their weights to minimize error and improve predictive accuracy. Gradient descent serves as an optimization algorithm that enables perceptrons to navigate the error landscape by finding the optimal set of weights.
During the training phase, the perceptron utilizes a loss function to determine the difference between the predicted output and the actual target. This loss function provides a quantitative measure of the performance of the perceptron. The goal of the learning mechanism is to minimize this loss, thereby improving model accuracy. Gradient descent operates by calculating the gradient of the loss function with respect to the weights, which indicates the direction and magnitude of weight adjustments necessary to minimize error.
Backpropagation complements gradient descent by facilitating the efficient computation of gradients. It achieves this through the chain rule of calculus, allowing the perceptron to update weights layer by layer, from the output layer back to the input layer. This process involves propagating the error backward through the network and adjusting the weights to reduce the error iteratively. Each adjustment is proportional to the derivative of the loss function concerning each weight, reducing the overall error in a controlled manner.
The interaction between gradient descent and backpropagation enables perceptrons to refine their geometry effectively. As weights are adjusted based on the computed gradients, the decision boundary that separates different classes in the data space transforms, thereby affecting the perceptron’s classification performance. This iterative process continues until the perceptron converges to a set of weights that minimizes the loss function, demonstrating a powerful interplay between geometry and learning in artificial neural networks.
Limitations of the Perceptron Model
The perceptron model, despite its historical significance in the development of artificial neural networks, has notable limitations that restrict its applicability in various domains. One of the primary challenges associated with perceptrons is their inability to solve non-linearly separable problems. A classic example of this limitation is illustrated by the XOR (exclusive OR) problem, where the data points cannot be separated using a single linear hyperplane. This means that while a perceptron can classify linearly separable data, it fails to address scenarios involving complex relationships between variables.
This limitation is not merely a theoretical concern; it reflects an essential aspect of real-world data, which is often non-linear in nature. In practical applications, data often contains intricate patterns that require more sophisticated models. The perceptron, with its single-layer architecture, lacks the capacity to learn such complexities. Consequently, many problems encountered in fields such as image recognition, natural language processing, and speech recognition cannot be effectively tackled using a simple perceptron model.
Moreover, the perceptron’s inability to represent multiple classes is another significant limitation. As it operates under a binary classification framework, it cannot directly manage scenarios where more than two classes are present. To address this shortcoming, the introduction of multi-layer perceptrons (MLPs) became essential, allowing for greater flexibility and capacity to learn from intricate patterns. Understanding these limitations is crucial as they shape the evolution of more advanced neural network architectures, leading to the development of algorithms capable of addressing complex challenges.
Advancements Beyond the Perceptron: Multi-layer Networks
The evolution of artificial neural networks has led to the development of multi-layer perceptrons (MLPs), which significantly improve upon the traditional single-layer perceptron architecture. While a single-layer perceptron is capable of solving only linearly separable problems, MLPs are designed to tackle more complex datasets by incorporating one or more hidden layers between the input and output layers. This additional structure enables the model to learn intricate patterns and representations that are either polynomial or non-linear in nature.
The architecture of an MLP typically consists of an input layer, one or more hidden layers, and an output layer. Each layer comprises multiple neurons, with each neuron in the hidden layers applying a non-linear activation function to its weighted input signals. The introduction of these non-linear activation functions, such as ReLU (Rectified Linear Unit), sigmoid, or hyperbolic tangent, allows MLPs to model a wider variety of functions. This non-linearity is crucial; without it, stacking multiple layers would merely replicate the function of a single-layer perceptron.
Training an MLP typically involves the backpropagation algorithm, which adjusts the weights of connections between neurons based on the errors in predictions. This iterative process allows the network to learn from its mistakes and refine its understanding over time. Consequently, MLPs have become a fundamental component of modern deep learning architectures, underpinning numerous applications ranging from image and speech recognition to natural language processing.
In light of these advancements, it becomes evident that multi-layer networks have transformed the landscape of neural computing. By overcoming the limitations of single-layer perceptrons, MLPs have ushered in a new era of capabilities, enabling more sophisticated and powerful models to emerge in the field of artificial intelligence.
Applications of ANN and Perceptron Geometry
Artificial Neural Networks (ANNs) have found extensive applications across various domains, benefiting significantly from an understanding of perceptron geometry. By leveraging the geometric properties of perceptrons, researchers can enhance the performance of neural networks in crucial areas such as image recognition, natural language processing, and data classification.
In image recognition, ANNs, particularly convolutional neural networks (CNNs), have demonstrated remarkable capabilities in accurately identifying and classifying objects within images. By analyzing the geometric relationships between pixels, these networks effectively learn to map complex visual features into spaces where they can be separated adequately. Understanding perceptron geometry allows for optimizing these mappings, leading to improvements in training efficiency and accuracy.
Natural language processing (NLP) is another domain where ANNs thrive. Here, semantic relationships between words are vital for tasks such as sentiment analysis, machine translation, and chatbot functionalities. ANN models utilizing perceptron geometry can better capture syntactic and semantic structures in language data. By organizing these relationships in high-dimensional spaces, systems become adept at discerning contextual meanings, leading to more nuanced interactions in conversational agents.
Moreover, the implications of perceptron geometry extend to other areas, including finance, healthcare, and autonomous systems. In finance, ANNs are employed for fraud detection or stock market predictions, where geometric properties enhance the classification capabilities of neural networks by improving pattern recognition in large datasets. In healthcare, they assist in diagnosing diseases from medical images or predicting patient outcomes through predictive modeling. The ability of ANNs to learn from geometric representations ultimately enhances their utility across diverse real-world applications.
By appreciating the intricacies of perceptron geometry, practitioners can leverage ANNs more effectively, leading to advancements in technology that are integral to current and future innovations.
Conclusion and Future Directions
Throughout this exploration of artificial neural networks (ANNs) viewed through the lens of perceptron geometry, several crucial concepts have been highlighted. Perceptrons, as foundational models, not only serve as the building blocks of machine learning but also encapsulate geometric insights that enhance our understanding of data representation. By illustrating how different configurations of perceptrons can segregate data in a multidimensional space, we have underscored the potential of geometry in the training and optimization of neural networks.
The field of artificial neural networks is witnessing significant advancements, particularly in relation to deep learning methodologies that employ intricate architectures composed of multiple layers of perceptron-like units. These models have achieved remarkable successes across various applications, from image recognition to natural language processing. The geometry of these networks plays an instrumental role in their effectiveness, as it facilitates a nuanced understanding of how data transformations occur at each layer.
Looking towards the future, ongoing research aims to improve ANN architecture by enhancing the interpretability and efficiency of models. This pathway includes exploring novel geometric constructs that could refine perceptron-like models, making them more adept at handling complex data. Furthermore, the integration of geometric principles into neural network training methods might lead to reduced computational requirements and improved learning processes.
As we stand at this crossroads within artificial intelligence, it is clear that the interplay between geometry and neural architectures will continue to influence the trajectory of research and innovation. There is substantial promise for further investigation into how these elements converge to yield even more proficient and versatile artificial neural networks, paving the way for groundbreaking applications in various fields.